Dinamik Programlama (Dynamic Programming) nedir?

Merhaba. Bu yazıda dinamik programlamayı olabildiğince açıklayıcı şekilde anlatmaya çalışacağım.

Dinamik Programlama Nedir?

Dinamik programlama karışık problemlerin daha basit düzeylere indirilerek çözülmesini esas alan bir optimizasyon yöntemidir. Optimizasyondaki amaç, problemdeki kısıtlayıcı koşullar altında bu problemle ilgili en iyi karara varmaktır. Bir problem üzerinde dinamik programlama uygulayabilmek için o problemin alt problemlere parçalanabilir veya bir önceki problemin karakteristiğini koruyacak şekilde çözümü daha kolay başka probleme dönüştürülebilir olması yeterlidir

Yönteme göre optimum çözüm başlangıç durumundan bağımsız olarak diğer çözümler ile çözüm sonuçlarına göre optimum çözümler ardışıklığıdır. Yani, başlangıçta alt problemlerin çözümü bulunup buradan elde edilen verilerle daha büyük alt problemler çözüldüğünde problemin kendisi de çözülmüş olmaktadır.

Nerelerde Kullanılır?

Dinamik programlama, aynı çözümlü küçük problemlere parçalanabilen tüm problemler için uygulanabilir. Fakat brute-force ile exponential zamanda çözülebilen problemlerde gerçek değerini gösterir. En basitinden fibonacci dizisinin hesabı $O(2^n)$ zaman karmaşıklığına sahipken, dinamik programlama ile problem $O(n)$ zamanda çözülebilmektedir.

DP ile çözülebilecek birkaç problem:

Rod-cutting problem
Knapsack problem
Matrix-chain multiplication
Assembly Line Scheduling
Birçok string problemi(LCS, longest increasing subsequence, Levenshtein distance)

Yapısı ve Kullanımı

Başlamadan önce, birazdan sıkça göreceğiniz memoization kavramına bakmanızı öneriyorum.

Dinamik Programlama Algoritmasının Kurulması

Bir problem için dinamik programlama algoritması yapmak için aşağıdaki dört adım uygulanır.

Characterize the structure of an optimal solution (En iyi çözümün karakteristiğinin belirlenmesi)
Recursively define the value of an optimal solution(En iyi çözümün özyinelemeli tanımı)
Compute the value of an optimal solution,typically in bottom-up fashion(En iyi çözümün değerini top-down with memoization veya bottom-up yaklaşımdan birini kullanarak hesaplanması(genel olarak bottom-up))
Construct an optimal solution from computed information(Hesaplanmış verileri kullanarak en iyi çözümü bul)

Yazılan dört adımın ilk üç adımı dinamik programlamanın temel üç adımıdır. Eğer optimal çözümün yalnızca değerine ihtiyacımız varsa(Ör: LCS probleminde eşleşen harf sayısı) yalnızca ilk üç adımı kullanmak yeterli olacaktır.

Farklı problemler için farklı algoritmalar kurulacağından, Rod-Cutting problemi üzerinden DP’yi anlatmaya çalışacağız.

Rod-Cutting problem (Çubuk kesme problemi)

Problem : $n$ uzunluğunda bir çubuğumuz olsun, bu çubuğun her $i$ cm lik parçasının $p_i$ gibi bir fiyatı olsun. $i$ uzunluğundaki bir çubuğun, kendinden küçük parçalarla oluşturulabilen max fiyatına da $r_i$ diyelim.Fiyat tablosu aşağıdaki gibi olduğuna göre, farklı $n$ uzunluğundaki çubukları kaç parçaya bölersek en fazla kar edeceğimizi bulalım.

$\begin{array}{c|ccccccccc} length(i) &1&2&3&4&5&6&7&8&9&10\\ \hline price(p_i) &1&5&8&9&10&17&17&20&24&30 \end{array}$

4 birimlik çubuk için soruyu çözecek olursak;

$9 = p_4 \not= r_4$
$9 = p_1+p_3 \not= r_4$
$10 = p_2 + p_2 ?= r_4$
$4 = p_1 + p_1 + p_1 + p_1 \not= r_4$
$7 = p_1 + p_1 + p_2 \not= r_4$ olur. Ve bu durumda en pahalı satışın çubuğu iki parçaya bölerek, $r_4 = p_2 + p_2 = 10$ şeklinde yapıldığını görebiliriz.

1- Characterizing a rod-cutting

Çubuğumuzu parçalayacağımız birimler $i = 1,2,\ldots,n-1,n$ gibi tam sayılar olduğundan ayrışmanın karakteristiğini belirleyebiliriz. Örneğin $7 = 2 + 2 + 3$ dersek, 7 birim uzunluğundaki çubuğu 2 adet 2cm ve bir adet 3cm olmak üzere 3 parçaya bölmüş oluruz. $i$ değerim en küçük $1$ en büyük $n$ olabileceğinden, parça sayısı $k$ ‘yı $1\lt k \lt n$ şeklinde gösterebiliriz.

Tüm parçaların uzunluklarını toplarsak, $n = i_1+i_2+\cdots+i_k$ elde ederiz.

Bir çubuğun en yüksek fiyatına $r_n = \max(p_1+r_{n-1} , p_2+r_{n-2},\ldots,p_{n-1}+r_1,p_n+0)$ şeklinde gösterebiliriz.

Burada, $r_n$ ‘i oluşturan her bir parça da kendini en pahalı yapacak parçalardan oluşmaktadır.

Genelleme yaparsak, maksimum çubuk fiyatı için şöyle diyebiliriz:

$r_n = \max_{1 \le i \le n}(p_i + r_{n-i})$

2- A Recursive solution

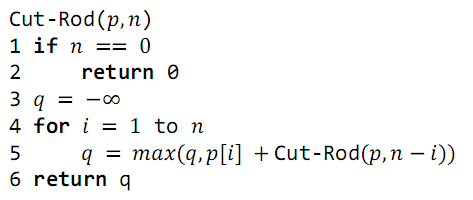
Yukarıdaki top-down recursive fonksiyon, genelleme yaparak bulduğumuz maksimum çubuk fiyatını geri döndürecektir.Dışarıdan $p[1..n]$ şeklinde ücretleri tutan bir tamsayı dizisi ve çubuk uzunluğunu tutan bir $n$ tamsayısı alır. $n == 0$ , fonksiyonun özyinelemesinin durmasını sağlayan kontroldür. Eşitlik sağlanmışsa $0$ döndürülür. Döndürülecek $q$ değerinin doğru olması için $q$ ‘ya en küçük ilk değer atanır. 5.satırda da bir for döngüsü ile her parça çağırılarak en büyük değer $q$ içine atılır. Problem çözümü için bu fonksiyonu kullanacak olursak, $O(2^n)$ zaman karmaşıklığı olduğundan $r_n$ çok uzun zamanda bulunabilecektir.

3- Compute the maximum value of a price

A. Memoization kullanılarak Top-Down yaklaşım ile

Memoized-Cut-Rod(p,n) fonksiyonu, asıl memoization işlemini yapan Memoized-Cut-Rod-Aux(p,n,r) fonksiyonunu çağırır. Bu fonksiyon içinde tanımlanan yardımcı array, bizi her defasında alt problem hesaplamaktan kurtarır.

Memoized-Cut-Rod-Aux(p,n,r) fonksiyonu recursive tanımladığımız Top-Down çalışan Rod-Cut(p,n) fonksiyonuna çok benzer. Farklı olarak ilk adımında dizi üzerinden kontrol yapar. Eğer bir alt problem daha önceden çözülmüşse, tekrar çözmeye gerek kalmadan değer doğrudan dizi üzerinden okunur. Çözülmemiş alt problem ise çözülerek dizi üzerine yazılır.

B. Bottom-Up yaklaşımı ile

Bottom-Up-Cut-Rod(p,n) fonksiyonunda $i$ problem boyutu $j$ alt problem boyutundan küçük olduğu sürece :

1. satırda alt problemlerin çözümünü tutabilmek için $r[0..n]$ dizisi yaratılır. Hemen altındaki satırda ise, hiç parça olmaması durumunun bir fiyatı olmayacağından $r[0]$ elemanına $0$ değeri atanır.

3. ve 6. Satırlar arasında $j$ büyüklüğüne sahip tüm at problemler çözülür. $j$ , $1$ değeriyle başlar ve $n$ olana kadar büyür. Bu sayede en küçük alt problemlerden büyüklere doğru bir çözüm elde etmiş oluruz.

6.satırda $r[j-i]$ de bulunan ücretle o an kontrol edilen ücretin toplamı ( $r[j-i]+p[i]$ ) ile $q$ , $q$ değerini maksimim yapacak şekilde karşılaştırılır, ve en büyük toplam $q$ ya atanır. 7. Satırda alt problem çözümleri güncellenir. 8. Satırda istenen değer geri döndürülür.

Dinamik programlama için kullandığımız Top-Down ve Bottom-Up yaklaşımların ikisi de asimptotik çalışma zamanına sahiptir. Bottom-Up-Cut-Rod fonksiyonunda iç içe iki for döngüsü olduğundan $O(n^2)$ çalışma zamanına sahip denebilir. Aynı şekilde, Memoized-Cut-Rod-Aux fonksiyonunun 6 ve 7. Satırlarına bakacak olursak, for içinde fonksiyonun kendini n kere çağırdığını görebiliriz. Özyineleme gerçekleşirken her alt problem yalnızca bir kere hesaplanacağından (memoization sayesinde) 7. Satırda çağıracağımız fonksiyon da bize n gibi bir karmaşıklık getirir. Dolayısıyla Memoized-Cut-Rod için de $O(n^2)$ çalışma zamanına sahip diyebiliriz.

4- Constructing a solution

Yukarıda yaptığımız hesaplamalar bize çözümü değil, yalnızca en iyi çözümün değerini getiriyordu. Eğer ihtiyacımız olan sadece bu değerse, fonksiyonu çağırmamızın ardından bize dönen değeri doğrudan kullanabiliriz. Eğer ki ihtiyacımız olan çözümün kendisiyse kullandığımız hesaplama(computing) algoritmalarından birini genişleterek çözümü de bir yerde tutacak hale getirmemiz gerekir. Bottom-Up-Cut-Rod fonksiyonun genişleterek çözüme gidelim.

Şeklinde bir genişletme ile çözüme ulaşabiliriz. Burada kullandığımız dizisi, tüm en iyi çözümleri içinde tutmaktadır.

Çözümün yazdırılmasını da aşağıdaki fonksiyonla yapalım:

Eğer fonksiyonumuzu Print-Cut-Rod-Solution( ) şeklinde verirsek aşağıdaki gibi bir çözümümüz olacaktır:

$\begin{array}{c|cccccccccc} length(i) &0&1&2&3&4&5&6&7&8&9&10\\ \hline r[i] &0&1&5&8&9&10&17&17&20&24&30\\ s[i] &0&1&2&3&2&2&6&1&2&3&10 \end{array}$

Longest Common Subsequance (En uzun ortak alt dizi)(LCS) problem

Problemin dinamik programlama ile çözümüne buradan ulaşabilirsiniz.

Algoritmanın iyileştirilmesi

Dinamik programlama sırasında birçok işlemi yeniden yapmak yerine alt problem çözümünü depoladığımızdan çözüme çok daha hızlı ulaşabiliriz. Fakat çok büyük problemler için bu bize büyük maliyette bir belleğe mal olabilir fibonacci sayısılarının bulunması, rod-cutting gibi problemler tek dizi üzerinde tutulduğundan $O(n)$ bellek kullanırken LCS, Matrix Chain Manipulation gibi problemler $O(n^2)$ bellek kullanırlar. Peki bu sorunun bir çözümü var mıdır?

Eğer bizden çözümün tamamı isteniyorsa maalesef yoktur. Fakat sadece çözümün değeri isteniyorsa çok küçük bellek kullanımlarıyla bu değer elde edilebilir. Örneğin, $35$ sayısına kadar olan tüm fibonacci sayılarını listeleyebilmek için dizinin tamamı elimizde olmalıdır. Fakat bizden $fib(35)$ değeri istenirse bunun için $fib(34)$ ve $fib(33)$ değerlerini bilmemiz yeterli olacaktır. Bu da $fib(35)$ değerine $O(1)$ bellek kullanarak ulaşabileceğimiz anlamına gelir. Aynı şekilde LCS probleminde bizden altdizinin ne olduğu yerine altdizinin uzunluğu istenirse, $O(n^2)$ yerine $O(n)$ bellek kullanarak değeri bulabiliriz.