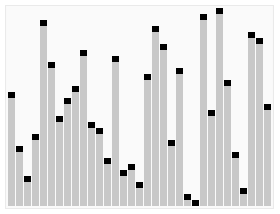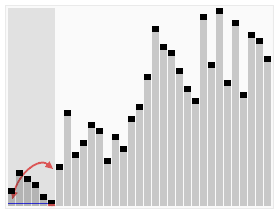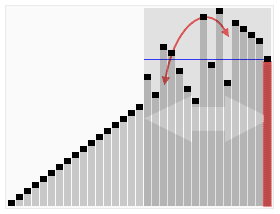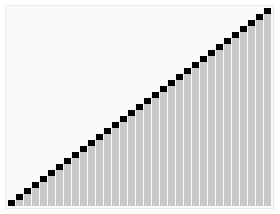
Quick sort (hızlı sıralama) sıralama algoritması, parçala ve çözümle (divide and conquer) mantığıyla çalışan, best-case O(nlogn), worst-case O(n^2) zaman karmaşıklığı ile en çok kullanılan sıralama algoritmalarındandır.
Algoritmayı şu üç adımla inceleyebiliriz.
- Liste içerisinden pivot olacak bir eleman seçilir.
- Pivot değerden küçük olanlar pivottan önce, büyük olanlar pivottan sonra olacak şekilde elemanlar liste içerisinde yer değiştirilir.
- Pivotun öncesindeki ve sonrasındaki değerler ayrı bir liste kabul edilip quick sort algoritması bu listeler için yeniden çalıştırılır.
Pseudocode :
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Quicksort(A[l..r]) | |
| //Alt dizilerin quicksort ile sıralanması | |
| //Input: Dizinin alt dizisi A[0..n − 1]eved | |
| // indices l and r | |
| //Output: Alt dizi A[l..r] artan şekilde sıralı | |
| if l < r | |
| s ← Partition(A[l..r]) //s : bölme pozisyonu | |
| Quicksort(A[l..s − 1]) | |
| Quicksort(A[s + 1..r]) |
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| public class QuickSort { | |
| public int[] sort(int[] numbers){ | |
| quickSort(numbers,0,numbers.length - 1); | |
| return numbers; | |
| } | |
| private void quickSort(int numbers[], int left, int right) { | |
| int index = partition(numbers, left, right); | |
| if (left < index - 1) | |
| quickSort(numbers, left, index - 1); | |
| if (index < right) | |
| quickSort(numbers, index, right); | |
| } | |
| // Pivot degerin solunda pivottan kucuk, | |
| // pivot degerin saginda pivottan buyuk | |
| // degerlerin olmasini saglar. | |
| // Geriye pivot'un dizi icerisindeki konumunu dondurur | |
| private int partition(int numbers[], int left, int right) | |
| { | |
| int i = left, j = right; | |
| // Pivot deger listenin ortasindan alinir | |
| int pivot = numbers[(left + right) / 2]; | |
| // Listenin iki degere bolunmesi | |
| while (i <= j) { | |
| // Pivottan kucuk degerler uzerinde olundugu surece donulur | |
| while (numbers[i] < pivot) | |
| i++; | |
| // Pivottan buyuk degerler uzerinde olundugu surece donulur | |
| while (numbers[j] > pivot) | |
| j--; | |
| // Pivot'un sagindaki kucuk deger ile solundaki buyuk deger yer degistirilir. | |
| if (i <= j) { | |
| int tmp = numbers[i]; | |
| numbers[i] = numbers[j]; | |
| numbers[j] = tmp; | |
| i++; | |
| j--; | |
| } | |
| } | |
| return i; | |
| } | |
| } |
